京都大學基礎物理學研究所博士課程學生白川雄貴、該研究所森前智行副教授以及NTT社會資訊研究所上席特別研究員(京都大學基礎物理學研究所特任副教授)山川高志的研究團隊,從密碼理論這一新視角證明了量子計算機比傳統計算機更快的「量子優越性」的必要充分條件。該研究成果已於6月27日在理論計算機科學國際會議「STOC 2025」上發表。
(供圖:京都大學)
人們期待量子計算機能快速解決傳統計算機需耗費大量計算時間的難題(量子優越性),但這種優越性並非始終存在。
研究團隊認為,要理解量子計算機性能並發揮其能力,必須明確回答「在何種條件下存在量子優越性」及「實現量子優越性需要什麼」等問題。
在數學上,當命題「A則B」與其反命題「B則A」同時成立時,我們說A與B互為必要充分條件。要證明量子計算機的優越性,就必須滿足這種必要充分條件。
迄今為止,例如針對採樣問題、搜尋問題等需要解決的問題,提出了量子優越性定義,並在特定條件下證明了其存在。但這些僅是充分條件,是否真正構成必要條件一直未被明確理解。
因此,此次研究為夯實量子優越性的理論基礎,著手解決「量子優越性的必要充分條件是什麼」這一根本問題。具體而言,團隊研究了近年量子密碼領域提出的「單向性謎題」這一密碼功能的安全性與量子優越性存在的關係,並從數學上證明了二者等價。
這種密碼是量子計算機生成的、傳統計算機無法破解的謎題。此外,等價性意味著如果密碼功能安全,則可構建展示量子優越性的任務,如果存在量子優越性,則可構造出安全的密碼功能。
此次成果通過整合量子計算理論與密碼理論各自發展的技術和思路,提出連接「量子優越性」與「密碼安全性」這兩個看似無關概念的新框架而得以實現。
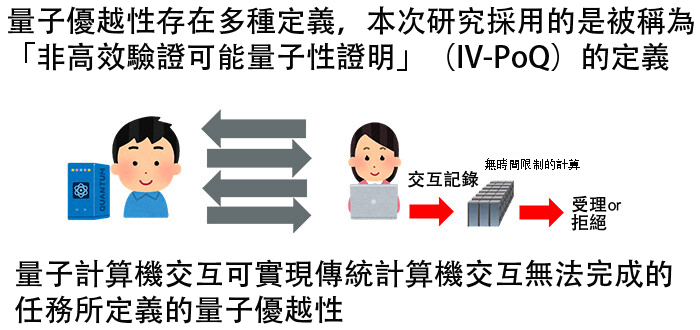
研究團隊特別關注了「非高效驗證可能量子性證明(IV-PoQ:Inefficient-Verifier Proofs of Quantumness)」這一互動式協議。該協議使不具備量子計算機的驗證者與擁有量子計算機的證明者交互,從而驗證對方是否真的具備量子計算能力。
研究從數學上證明了該協議存在的必要充分條件與「單向性謎題」這一密碼功能的安全性一致,從理論上揭示了量子優越性與密碼安全性具有等價關係。
研究團隊指出,此次成果的意義不僅在於明確了量子優越性的必要充分條件,還在於量子計算理論與密碼理論間存在的這種關聯性有望對兩個領域產生相互影響。
其意義之一在於,未來量子優越性的實證實驗與理論研究將在更堅實的密碼理論基礎上推進。之二是這一成果意味著「如果量子優越性不存在,則當前多數被視為安全的密碼功能將面臨安全性崩塌」。
這種安全性崩塌風險不僅涉及量子密碼,更將波及當前廣泛使用的傳統計算機密碼及亟待普及的抗量子計算機密碼,對資訊安全領域具有重大啟示意義。
原文:《科學新聞》
翻譯:JST客觀日本編輯部
【論文資訊】
期刊:Proceedings of the 57th Annual ACM Symposium on Theory of Computing
論文:Cryptographic Characterization of Quantum Advantage
DOI:10.1145/3717823.3718133













